

In the "flux-qubit" team, we study mesoscopic superconducting circuits containing tunnel junctions in order to use them as building blocks for a quantum computer.
We acknowledge support from the following institutions

|

|
THE "PERSISTENT-CURRENT" QUBIT
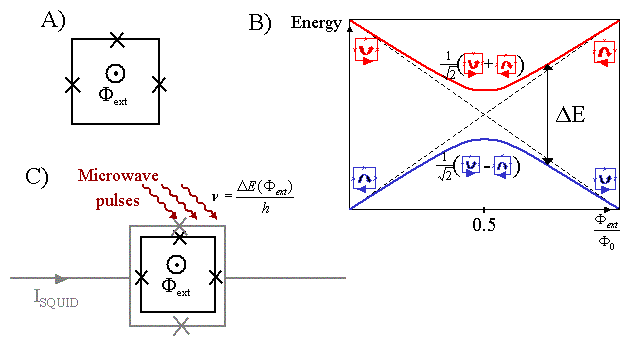
Fig. 2 : A) The
persistent-current qubit is a three-junction loop biased by an external flux. B)
Low-energy diagram of the persistent-current qubit C) Detection (in gray) and
manipulation (in purple) of the qubit.
We observed the coherent dynamics of a persistent-current qubit. In this
sample, the three-junction loop and the detection Squid share a common branch as
can be seen on the SEM-picture of figure4. We used microwave pulses of variable
length and amplitude to coherently manipulate the quantum stateof the loop. The
readout by the Squid was also pulsed and revealed quantum-state oscillations
with high fideity (see figure 4).Under strong microwave driving, it was possible
to induce hundreds of coherent oscillations. We could performRabi, Ramsey and
echo-type sequences. We measured a relaxation time of 900 nanoseconds and a
free-induction dephasing time of 20 ns. [6] To learn more about this
experiment, click.
Inductive measurement of a qubit Switching of the measuring DC-SQUID to the finite voltage state strongly perturbs
the measurement circuit and the qubit. We investigate a method for the readout of a flux
qubit based on a direct measurement of the Josephson inductance of the DC-SQUID. The
DC-SQUID is shunted by a capacitor, such that the plasma frequency is in the range
0.5-1 GHz (see fig. 5A). Close to the resonance frequency of this circuit the output voltage is very
sensitive to the flux produced by the qubit. We have characterized this method and
measured the state of a persistent current qubit, obtaining a relaxation time of the
order of 80 ms (see figure 5B). The fidelity of the measurement is 70%, being limited at this stage by
the amplifier added noise.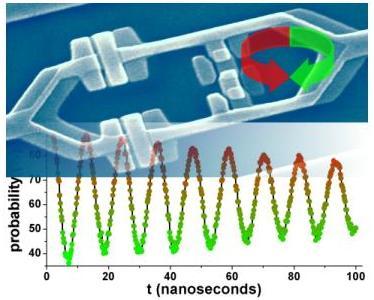
Fig. 4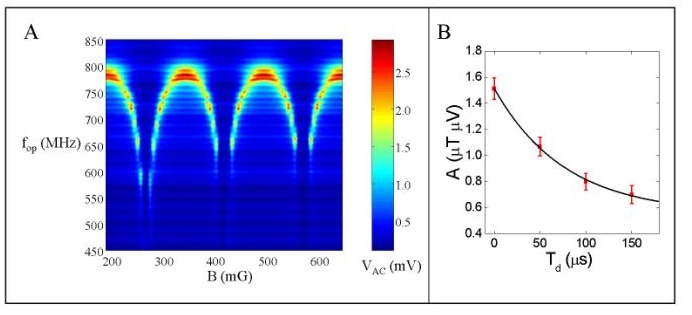
Fig. 5
Epitaxial Josephson junctions
Up to now, the Josephson junctions in the superconducting circuits were fabricated with two-angle shadow evaporation. This technique is easy to use and standard practice for making sub-micron structures. However, the reproducibility of the junctions is limited, as the junction region is non-planar and the area is therefore poorly defined. As the sample is covered with resist during evaporation, cleaning the surface by heating is not possible and resist outgassing might also limit the junction quality. In particular, fluctuations in the critical current density make it difficult to achieve more complex qubit circuits. Critical current noise due to impurities in the barrier may lead to additional decoherence. Therefore we try to establish a fabrication scheme based on epitxially grown Al/Oxide/Al trilayers. Single-crystalline aluminum films and trilayers have been grown already. The TEM picture (figure 6A) shows the lattice planes of the aluminum films. The oxide layer in between is also very uniform. Presently, we are setting up a fabrication procedure for making sub-micron Josephson junctions out of these trilayers (see figure 6B).
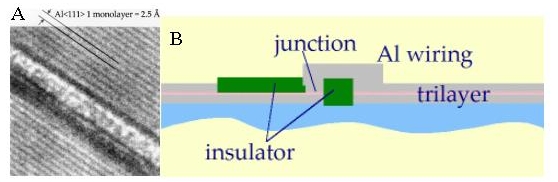
Fig. 6
[1] W. J. Elion et al., Nature 371, 594 (1994)
[2] J. M. Martinis et al.
, PRB 35, 4682 (1987)
[3] Y. Nakamura, Y. Pashkin, J. Tsai, Nature 398, 786
(1999)
[4] J. E. Mooij et al., Science 285, 1036 (1999)
[5] C. H. van
der Wal et al., Science 290, 773 (2000)
[6] I. Chiorescu, Y. Nakamura, C. J.
P. M. Harmans, J. E. Mooij, published online in Science : 13 February 2003 10.1126/science.1081045