|
This page is about my PhD-research on superconducting flux qubits ('quantum bits'), also called persistent-current qubits,
performed in the flux-qubit team of the Quantum Transport Group of Prof. J.E. Mooij and Dr. C.J.P.M. Harmans at the
Physics department of Delft University of Technology in the Netherlands.
The goal of this research is to understand behaviour of macroscopic quantum mechanics at a fundamental level, as well as investigating the possibilities for building a quantum computer.
Index of this page:
1) Macroscopic Quantum States in superconducting circuits
2) Principle of the Flux Qubit
3) Spectroscopy of the qubit
4) Coherent manipulation of superconducting quantum bits
5) Coupling of qubits
6) Coherent operations on a Coupled qubit system
7) Colleagues
Macroscopic Quantum States in superconducting circuits
Ever since quantum mechanics was shown to be successful in explaining the way atoms work in the beginning of last century the limits of its validity have been
investigated. Schrodinger's famous thought experiment consists of a microscopic
two-state system, for which quantum mechanics is supposed to be valid, linked
to a macroscopic system (for example a cat), which is supposed to behave classically,
in such a way that the fate of the cat ('alive' or 'dead') is linked to the state of the
quantum two state system (|0> or |1> ). The conclusion that a superposition of the
quantum system would lead to a superposition of the cat's fate was the beginning
of numerous discussions about the interpretation of quantum mechanics.
It was experimentally confirmed that indeed quantum mechanics has some remarkable features which are unknown in classical mechanics.
Long distance entanglement between photons was demonstrated in EPR experiments, and tests of Bell's inequalities have shown that quantum correlations are larger than would be possible in classical systems. This peculiar behaviour leads to the question how the classical world emerges from the microscopic quantum world.
Numerous experiments were proposed to investigate this issue. The use of superconducting
devices was proposed to test the idea that one can make superpositions
of macroscopic flux states. Some other remarkable experiments include
an interference experiment in which the path-information can be erased after the
photon has passed the double slit, and an experiment showing interference
patterns not using electrons or photons but using large molecules .
During my PhD research I investigated (together with my colleagues) macroscopic quantum mechanics by looking at the behavior of quantum states in superconducting circuits.
The system we investigate consists of a superconducting aluminum loop intersected by three Josephson junction as our quantum system. We use a DC SQUID coupled to the qubit to measure the flux generated by the persistent currents flowing through the ring depending on its state.
The system can be exited from the groundlevel to the excited state using microwave radiation in the GHz-range, thus probing the quantum-states of the system. In this way, using continuous RF radiaton, spectroscopy methods are used to map out the energy level spectrum of a single or coupled qubit system.
Using nanosecond pulses, we performed coherent manipulation of single qubits systems and coupled two-qubit systems, showing the feasibility of two-qubit operations for usage in quantum computation, and for further experiments on entangled systems.
Superconducting Circuits as Quantum Bits or qubits
Superconducting systems in either the flux or charge regime are seen as candidates for use in future quantum computation. Any usable quantum computer should consist of a number of quantum bits (qubits) that can be coupled and decoupled at will. The easiest way to couple flux-qubits is by using the flux produced by the qubits depending on the state it is in. In this way σzσz coupling can be achieved.
However, decoherence will be the main obstacle to coherent manipulation on any many-qubit system used as a 'Quantum Computer', and experiments performed on single and two-qubit flux systems indicate decoherencetimes are in the order of microsecond for relaxation (T1) and only ten to hundreds of nanoseconds for the dephasing (T2) of the system. It is this dephasing which puts a limit on the time there is to perform any (usefull) manipulation of those systems, and increasing the dephasing time is therefor one of the great challenges for quantum computers build of superconducting flux qubits.
Principle of the Flux Qubit
The Josephson Persistent Current Qubit or Flux Qubit consists of a loop containing three junctions, see figure A.
When biased at a flux Φ around Φ0/2, the qubit has two low-energy levels. If Φext is far from Φ0/2,
the two energy eigenstates carry a mesoscopicsupercurrent (typically 300nA) which flows either clockwise or anticlockwise. If Φ=Φ0/2, the energy eigenstates are coherent superpositions of the two current-carrying states.
One can induce a transition between those two levels by applying microwave radiation at the resonance frequency. Typical level splitting is in the order of a few Gigaherts near the degeneracy point, for a qubit with circulating currents in the order of a few hundred nanoamps.
We use a DC SQUID coupled to the qubit to measure the flux generated by the persistent currents flowing through it, and thus to detect its state after all coherent operations are performed.

Figure 1:Electron Microscope picture of a Josephson persistent current qubit (inner loop) and the measurement-SQUID (outer loop). The inner loop contains three Josephson Junction with a critical current of a few hundred nA. When biased at a flux of Φ0/2 the system will effectively behave as a two state system, with classical states corresponding to either a left or right circulating current in the loop. The DC-SQUID can be used to measure the flux produced by the qubit.
This is a picture of the first qubit we fabricated and performed spectroscopy-experiments on, back in 1999/2000, see this 'Quantum Superposition of Macroscopic Persistent Current States' article in Science.
I fabricated this structure in the DIMES cleanroom of Delft University; The Josephson junctions are created using a technique called 'shadow evaporation' of aluminum.
Spectroscopy of the qubit
Spectroscopic measurements fully confirmed the expected energy diagram.
The measurements shown are performed on a qubit similar as the one in the SEM picture shown in figure 1.
We measured the average switching current of the SQUID as a function of the external flux while applying CW microwave.
Figure 2a shows the data for different microwave frequencies.
The peaks and dips result from transition between the two energy levels of the qubit.
In figure 2b the microwave frequency as a function of the external bias flux is plotted.
As expected from quantum mechanical analisys of the circuit,
the transition frequency varies linearly at large bias fields, and exhibits an anti-crossing around Φ0/2.
This is an indirect proof that a coherent superposition of crrent states was achieved.
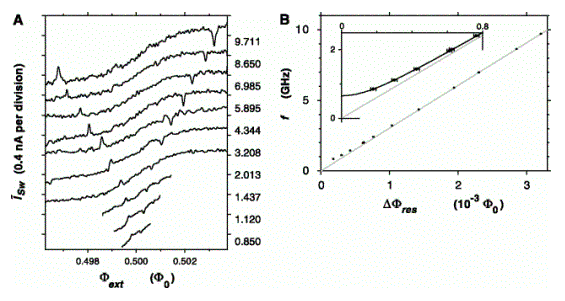
Figure 2:Spectroscopy on a superconducting flux qubit
Coherent manipulation of superconducting quantum bits : Measurement of Rabi oscillations
We use microwave pulses at a time scale of nanoseconds to induce so called Rabi-oscillations in the qubit system.
Figure 3 shows measurements of Rabi-oscillations measured using a SQUID magentometer.
The length of the microwave pulse is varied between 1 ns and 150 ns, and for each pulselengt the switching probability of
the SQUID is measured.
We induce Rabi oscilations by applying an oscillating magnetic field of a frequency matching the level splitting of the qubit energy levels by using an on-chiop microwave line fabricated next to the qubit. The measured value is the switching probability of the SQUID magnetometer surrounding the qubit.
Measured dephasing times in a driven system are in the order of hunderd nanoseconds, as can be seen from those measurements. However, the dephasing time measured using Ramsey-interference is much shorter, giving a free-decay time of the phase coherence in the order of tens of nanoseconds. Identifying the sources for the dephasing is one of the challe
nges that have to be adressed before flux qubits can be utilised for experimental tests of quantum computation.
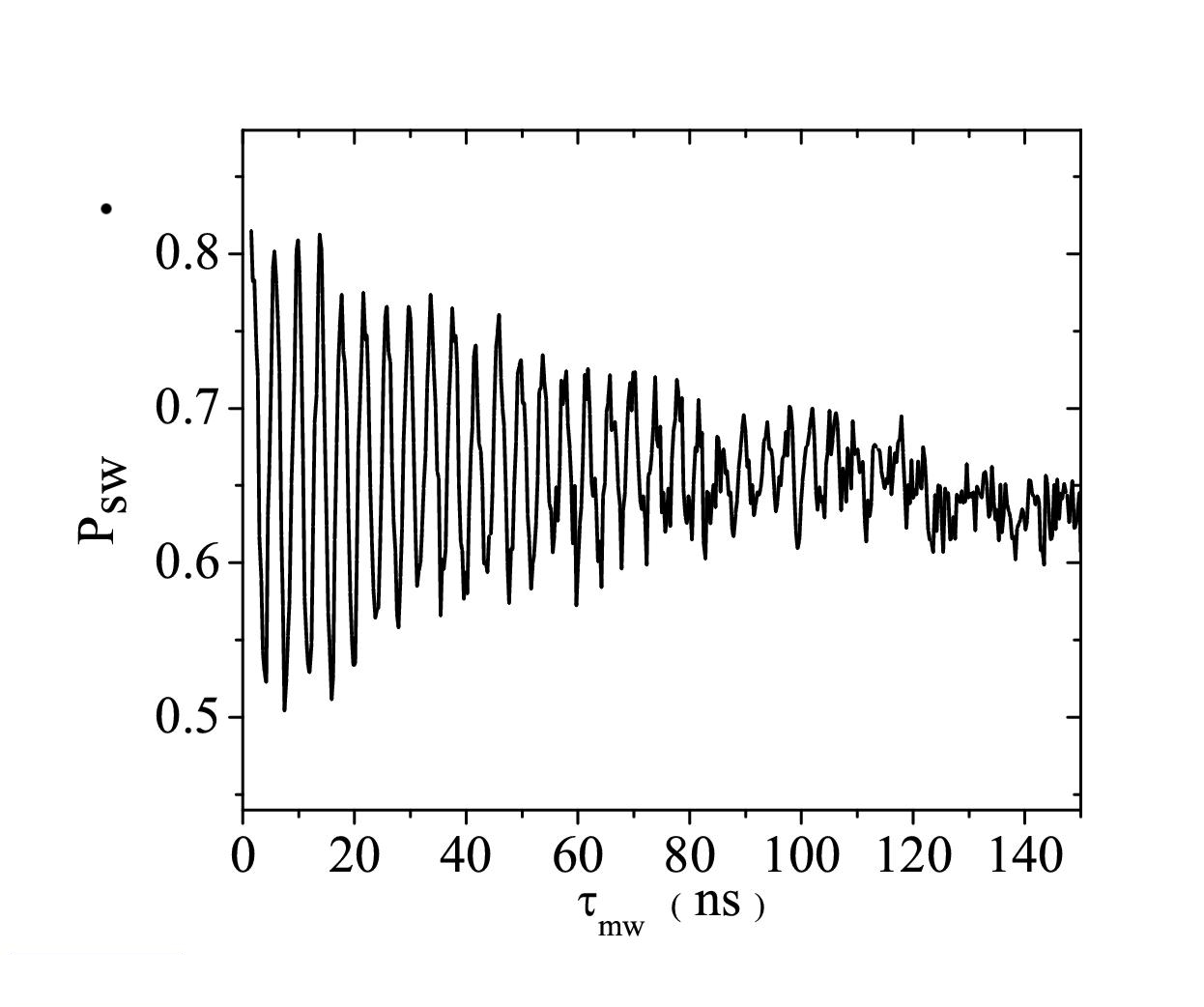
Figure 3:Rabi oscillations between the two lowest energy levels of a supoerconducting flux qubit near the degeneracy point. The state of the qubit ψ = α|0>+ β|1> oscillates as a function of the length of the perterbation for pulses up to 100 nanoseconds.
Figure 4 shows Rabi-oscliations for various powers (amplitudes) of the applied perturbation (the magnetic radiation applied to the qubit.
The measured traces nicely show the expected decrease in Rabi-frequency when power decreases. From the data it is clearly visible that the dephasing of the driven oscilations also decreases when the driving power is decreased.
This is a sign that the free decay time (the dephasing time measured by for example an echo-experiment) is lower then the dephasing-time of a system driven by a high amplitude.
Current research has a phocus on significantly increasing the dephasing time by controlling the environment of the qubit system. One of the possible causes of dephasing is fluxnoise. Also chargefluctuations on the superconducting islands or in the junction region can be a cause of dephasing.
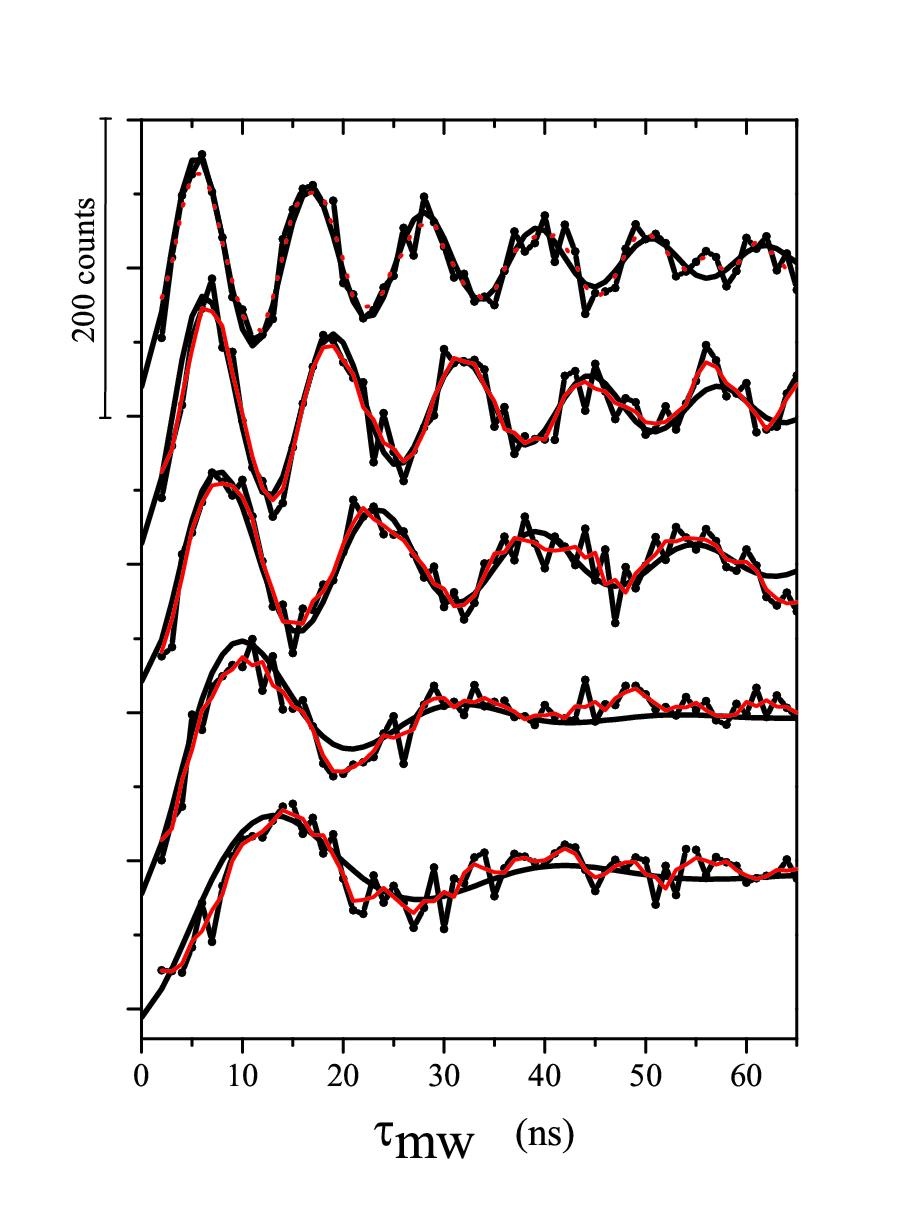
Figure 4:Rabi oscilations decreasing with amplitude of the applied radiation.
Coupling of qubits
Coupling of flux-qubits can be achieved using the flux degree of freedom by putting them next to eachtother. The fluxstate of one qubit (up or down) will shift the resonance frequency of the other qubit, shifting the other qubit in or out of resonance.
Figure D shows an electron microscope picture of two coupled qubits. The measurement SQUID in this case surrounds both qubits, meaning that the measured signal is the combined flux produced by the two qubits together. The qubits are coupled via their shared line as shown in the picture. The couplingstrength is fixed and is determined by the mutual inductance between the loops, consisting of both the geometric induction Mgeo and the kinetic induction Mkin of the shared line. The coupling energy is given by J= MI1I2, where M= Mgeo+ Mkin. The superconducting systems used in our experiments have a shared line of a few micrometers, linewidths in the order of 100-200nm, and a layerthickness of 80nm, giving typical values of the mutual inductance M in the order of 10-12H, where both kinetic inductance and geometrical inductance are in the same order of magnitude. In reality it is even a bit more complicated: Due to the shadow evaporation technique used in fabrication, the current of one qubit mainly flows through the upper layer of the shared line, and the current of the other qubit through the lower layer. Both layers are in effect sepparated by a large ditributed Josephson junction.

Figur 4:Two coupled qubits. Coupling is achieved via the shared line. Both the geometrical induction and the Josephson
induction of the superconducting line contribute to te coupling.
More on this can be found in this article (PRL, 2005).
Coherent operations on a Coupled qubit sample
More details about the measurements performed by me and my collegues on single and coupled qubits,
and more details about how to describe the Hamiltonian of the coupled qubit system using the Lagrange formalism, and description using around the degeneracy point using the simplified two-level aproximation can be found in my PhD-thesis (proefschrift) or on some of the other links.
Collegues at QT
The work shown here on coupled qubits was performed in the Flux qubit group of Jans Mooij and Kees Harmans.
I enjoyed working with many colleagues and visitors in the fluxqubit team at the TU Delft.
|




